Exploring applications of quantum computing
We are working to apply our expertise in quantum computing to identify applications of both commercial and research interest. The first step in finding applications is to understand the expected timeline of quantum computing. In our group, our focus so far has been on developing a detailed blueprint for a large-scale ion trap fault tolerant quantum computer, which would be capable of running the most powerful quantum algorithms, such as Shor’s for breaking RSA encryption. We are now also investigating near term devices and their potential applications.
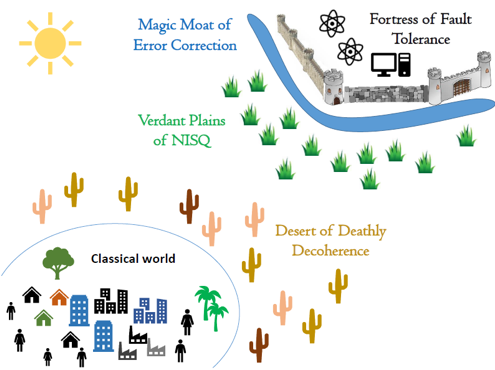
Image credit Ewan Munro, https://medium.com/@quantum_wa/quantum-computing-near-and-far-term-opportunities-f8ffa83cc0c9 inspired by Daniel Gottesman
The above figure illustrates the expected timeline of development for quantum computing. As we exit the classical world of computing we enter the desert of deathly decoherence, which represents the period at which we now have control over quantum systems, such as isolating and manipulating individual qubits, but this control is not sufficient to run algorithms which may compete with classical computing. Many experts would agree that the development of control in recent years signifies us now (2019) moving into the Verdant Plains of NISQ (Noisy Intermediate Scale Quantum), where the first useful applications will begin to arise. Specially tailored algorithms sometimes referred to as Hybrid Quantum Computing are designed to run on NISQ devices, where the noise of the device places an upper limit on the length algorithm which can be run.
The most powerful quantum algorithms, among which some promise an exponential speed up, will require an error corrected (fault tolerant) device. Fault tolerance devices can run arbitrarily long algorithms due to their error correction techniques, but this necessitates a large overhead of physical to logical qubits, approximately 1000:1. This large qubit overhead is represented in the diagram by the magic moat of fault tolerance. We will spend years in the Verdant Plains of NISQ before we have the ability to scale to the required qubit numbers which would enable a fault tolerance device.
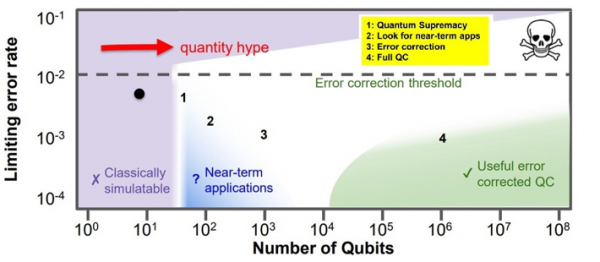
Illustration of the qubit quality vs quantity relationship. Image credit: John Martinis, Google. (taken from https://medium.com/@quantum_wa/quantum-computing-near-and-far-term-opportunities-f8ffa83cc0c9 )
The above figure is a quantified version of the previous timeline. An additional feature highlighted by this figure is the concept of quantity hype. Often the number of qubits in a device is stated as a measure of its power, but in the situation where the error rate of a device is so high that one cannot run an algorithm of any appreciable length, is it fair to call them qubits? The computation power of a NISQ device must be a function of both the number of qubits and the limiting error rate.
The difficulty of Quantum Chemistry (simulating atoms and molecules) scales exponentially with the problem size on a classical computer, which means that it quickly becomes impractical to solve problems of a certain size. A notable problem within quantum chemistry is on improving the efficiency of the Haber – Bosch process. Currently 2% of the world’s energy is spent on this process to create fertiliser by extracting nitrogen out of the air and converting it into ammonia. We know the method can be improved because it is a process that many bacteria do at a substantially higher efficiency. Simulating the necessary molecules to investigate this problem is beyond the capabilities of classical computers but it is hoped that a NISQ device will one day make headway. The quantum variational eigensolver is a hybrid quantum algorithm designed to run on NISQ devices and it promises an exponential speedup versus classical methods.
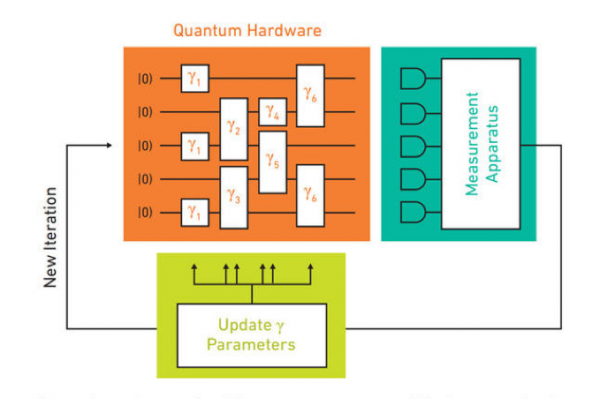
Located at: https://www.futurelearn.com/courses/intro-to-quantum-computing/0/steps/31581 , image credit “” Quantum Information and Computation for Chemistry 2016 ” p.10 http://aspuru.chem.harvard.edu/nsf-report/”
The above figure illustrates how hybrid quantum computing works. The quantum device runs a very short circuit (algorithm), and the answer is input into a classical optimiser. The classical optimiser then dictates the exact form of the next quantum algorithm to be run, and this process is iterated many times. This method avoids the algorithm length restriction of noisy devices while still utilising the power of a quantum computer.
In the near term, NISQ devices and adiabatic devices may impact the financial industry in areas such as portfolio optimisation, where the real time nature of the market places upper limits on the time which can be dedicated to the optimisation algorithms. Even minor advantages in this industry can lead to huge financial returns.
A fault tolerance quantum computer promises an even wider array of applications. The HHL algorithm for solving systems of linear equations exponentially faster than classical alternatives may have a huge impact on the field of machine learning. The quantum projective simulation algorithm, which has many similarities to neural networks promises a quadratic speedup and may have implications for AI.
